Measures of Dispersion
Introduction:
Measures of dispersion are descriptive
information that explains how connected set of scores are comparable to each
other. Statistician know the dispersion
as variability, scatter, or spread. Dispersion
is contrasted with location or central
tendency, and together
they are the most used properties of distributions. Using dispersion, a person
can easily interpret how stretched or squeezed is a distribution . The most
common measures of statistical dispersion are the variance, standard deviation and interquartile range.
A measure of statistical dispersion is
a nonnegative real number that is zero if all the data are the same and increases
as the data become more diverse. Most measures of dispersion have the same units as the quantity being measured. In
other words, if the measurements are in meters or seconds, so is the measure of
dispersion. Dispersion is very sensitive to outliers and does not
use all the observations in a data set. It is more informative to provide the
minimum and the maximum values rather than providing the range.
Standard Deviation:
Standard deviation (SD) is the most
commonly used measure of dispersion. It is a measure of spread of data about
the mean and it is the square root of sum of squared deviation from the mean
divided by the number of observations. In Statistics we have two formulas to
calculate SD.
1. For sample SD:
In sample SD formulas we use n - 1 instead of n in
the denominator, because this produces a more accurate estimate of sample SD.
2. For population SD:
Range:
This spread
measure, which is sometimes used , is defined as the difference between the
highest and lowest values.
Interquartile range:
This measure is defined as the difference
between the 1st and 3rd quartiles.
Variance:
Variance is
defined as the measure obtained by adding together the squares of the deviation
of the sample values from their mean, and dividing the result by the number of
values in sample.
We calculate the Variance as:
1.For Sample Variance:
2. For Population Variance:




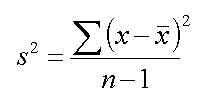


.bmp)
.bmp)
