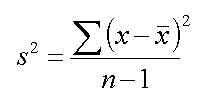Skewness

Skewness:

In Statistics we have numerous distribution and every distribution has his own graph and interpretation. Likewise, in skewness we use central tendency (Mean, Mode, Median) and construe it accordingly. Therefore, skewness is a tool that assist us to interpret  central distribution or central location through  following three ways:

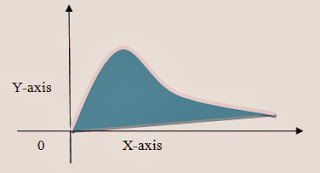
Positively Skewed:

In positively skewed, mean is always greater as compare to mode, median and mode is always less then median. In mathematically we can write it as:

Mean > Median> Mode = Mode< Median< Mean

Here graph shows that the data is Positively skewed and has right tail.

Negatively Skewed:

In negatively skewed, mode is always greater as compare to mean and median, mean is always less then median. In mathematically we can write it as:

Mean < Median < Mode = Mode >Median > Mean

Here graph shows that the data is Natively skewed  and has left tail.

Symmetric  or Skewed:

In symmetric or skewed, mean, mode and median are equal to each other and it has no tail.

Mean = Mode=Median

Here graph shows that the data is symmetric.

Measures of dispersion

Measures of Dispersion
Introduction:

Measures of dispersion are descriptive information that explains how connected set of scores are comparable to each other. Statistician know the  dispersion as  variability, scatter, or spread. Dispersion is contrasted with location or central tendency, and together they are the most used properties of distributions. Using dispersion, a person can easily interpret how stretched or squeezed is a distribution . The most common measures of statistical dispersion are the variance, standard deviation and interquartile range.

 

A measure of statistical dispersion is a nonnegative real number that is zero if all the data are the same and increases as the data become more diverse. Most measures of dispersion have the same units as the quantity being measured. In other words, if the measurements are in meters or seconds, so is the measure of dispersion. Dispersion  is very sensitive to outliers and does not use all the observations in a data set. It is more informative to provide the minimum and the maximum values rather than providing the range.

 

Standard Deviation:

Standard deviation (SD) is the most commonly used measure of dispersion. It is a measure of spread of data about the mean and it is the square root of sum of squared deviation from the mean divided by the number of observations. In Statistics we have two formulas to calculate SD.

1. For sample SD:

In sample SD formulas we use n - 1 instead of n in the denominator, because this produces a more accurate estimate of sample SD.

2. For population SD:

 

 

  Range:

This spread measure, which is sometimes used , is defined as the difference between the highest and lowest values.

 

 

Interquartile range:

This measure is defined as the difference between the 1st and 3rd quartiles.

 

Variance:

Variance is defined as the measure obtained by adding together the squares of the deviation of the sample values from their mean, and dividing the result by the number of values in sample.

We calculate the Variance as:

1.For Sample Variance:

2. For Population Variance: